Use our free Praxis Core Math practice test to review the most important skills and concepts that you must know for your certification exam. The Praxis 5733 Core Math test includes 56 questions that must be answered within 85 minutes. The test covers 4 major topics: Numbers & Quantities, Algebra & Functions, Geometry, Statistics & Probability. You may use a calculator.
Congratulations - you have completed .
You scored %%SCORE%% out of %%TOTAL%%.
Your performance has been rated as %%RATING%%
Your answers are highlighted below.
Question 1 |
Solve for $x$:
$3(x + 1) = 5(x − 2) + 7$$−2$ | |
$2$ | |
$\dfrac{1}{2}$ | |
$3$ | |
$−3$ |
Question 1 Explanation:
The correct answer is (D). Begin by distributing the $3$ and the $5$ through their respective parentheses, then combine like terms on each side of the equal sign:
$3(x + 1) = 5(x − 2) + 7$
$3x + 3 = 5x − 10 + 7$
$3x + 3 = 5x − 3$
Add $3$ to both sides to maintain the equality:
$3x + 6 = 5x$
Subtract $3x$ from both sides and then divide the resulting equation by $2$ to solve for $x$ as follows:
$6 = 2x$
$3 = x$
$3(x + 1) = 5(x − 2) + 7$
$3x + 3 = 5x − 10 + 7$
$3x + 3 = 5x − 3$
Add $3$ to both sides to maintain the equality:
$3x + 6 = 5x$
Subtract $3x$ from both sides and then divide the resulting equation by $2$ to solve for $x$ as follows:
$6 = 2x$
$3 = x$
Question 2 |
Which of the following numbers is the greatest?
$\dfrac{2}{3} ~~ 0.6 ~~ \dfrac{13}{22} ~~ 0.08$$\dfrac{2}{3}$ | |
$0.6$ | |
$\dfrac{13}{22}$ | |
$0.08$ |
Question 2 Explanation:
The correct answer is (A). To determine which value is the greatest, convert the fractions to decimals and compare each value. The fraction $\frac{2}{3}$ is equivalent to $2 ÷ 3$ or $0.66$; the fraction $\frac{13}{22}$ evaluates to $0.59$.
Question 3 |
Liam is driving to Utah. He travels at $70$ kilometers per hour for $2$ hours, and $63$ kilometers per hour for $5$ hours. Over the $7$ hour time period what was Liam's average speed?
64 km/h | |
65 km/h | |
66 km/h | |
67 km/h | |
68 km/h |
Question 3 Explanation:
The correct answer is (B). To find the average, use the following formula:
$\text{Average Speed} = \text{Total Distance} ÷ \text{Total Time}$
Total Distance $= 2 \text{hours} × 70 \text{km/h} + 5 \text{hours} × 63 \text{km/h}$
$= 140 \text{km} + 315 \text{km}$
$= 455 \text{km}$
Total Time $= 7$ hours
Average Speed $= 455 \text{km} ÷ 7 \text{hours}$
$= 65 \text{km/h}$
$\text{Average Speed} = \text{Total Distance} ÷ \text{Total Time}$
Total Distance $= 2 \text{hours} × 70 \text{km/h} + 5 \text{hours} × 63 \text{km/h}$
$= 140 \text{km} + 315 \text{km}$
$= 455 \text{km}$
Total Time $= 7$ hours
Average Speed $= 455 \text{km} ÷ 7 \text{hours}$
$= 65 \text{km/h}$
Question 4 |
Sofía's Restaurant offers the following choices:
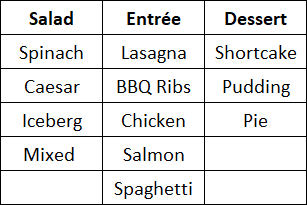If the only dinner you can order must include one salad, one main course, and one dessert, how many different combinations of this dinner are possible?
12 | |
60 | |
120 | |
144 | |
360 |
Question 4 Explanation:
The correct answer is (B). This can be solved with the Counting Principle: If there are $m$ ways for one activity to occur and $n$ ways for a second activity to occur, then there are $m × n$ ways for both to occur.
To solve this problem multiply:
$4 \; (\text{the number of salads})$ $× 5 \; (\text{the number of main courses})$ $× 3 \; (\text{the number of desserts})$:
$4 × 5 × 3 = 60$ different combinations
To solve this problem multiply:
$4 \; (\text{the number of salads})$ $× 5 \; (\text{the number of main courses})$ $× 3 \; (\text{the number of desserts})$:
$4 × 5 × 3 = 60$ different combinations
Question 5 |
If $4x + 3x − 2(x + 5) = −9$, then $x =$ ?
$−\dfrac{1}{2}$ | |
$−\dfrac{14}{5}$ | |
$−\dfrac{19}{5}$ | |
$\dfrac{1}{5}$ | |
$\dfrac{2}{3}$ |
Question 5 Explanation:
The correct answer is (D). Evaluate the expression by first distributing the −2 through the parentheses and then combining like terms:
$4x + 3x − 2x − 10 = −9$
$7x − 2x − 10 = −9$
$5x = 1$
$x = \dfrac{1}{5}$
$4x + 3x − 2x − 10 = −9$
$7x − 2x − 10 = −9$
$5x = 1$
$x = \dfrac{1}{5}$
Question 6 |
Li wants to buy as many bags of mulch as possible with his $\$305$, and he would like them to be delivered to his house. The cost is $\$7.50$ per bag and there is a $\$35.75$ delivery charge. The mulch is only sold in full bags. How many bags can Li buy?
35 | |
36 | |
40 | |
46 | |
41 |
Question 6 Explanation:
From Li’s initial amount of \$305, a flat \$35.75 delivery charge is deducted:
$\$305 − \$35.75 = \$269.25$
We can then divide this amount by the cost per bag to find the total number of bags that Li can buy:
$\$269.25 ÷ \$7.50$ $ = 35.9 \text{ bags}$
However, the question states that the mulch can only be sold in full bags, so we must round our answer down to ensure that Li does not exceed his budget.
$\$305 − \$35.75 = \$269.25$
We can then divide this amount by the cost per bag to find the total number of bags that Li can buy:
$\$269.25 ÷ \$7.50$ $ = 35.9 \text{ bags}$
However, the question states that the mulch can only be sold in full bags, so we must round our answer down to ensure that Li does not exceed his budget.
Question 7 |
Mason earns \$8.10 per hour and worked 40 hours. Noah earns \$10.80 per hour. How many hours would Noah need to work to equal Mason’s earnings over 40 hours?
15 | |
25 | |
27 | |
28 | |
30 |
Question 7 Explanation:
The correct answer is (E). Begin by calculating Mason’s total earnings after 40 hours:
$40 \text{ hours} × \$8.10 \text{ per hour} = \$324$
Next, divide this total by Noah’s hourly rate to find the number of hours Noah would need to work:
$\$324 ÷ \$10.80 \text{ per hour} $ $ = 30 \text{ hours}$
$40 \text{ hours} × \$8.10 \text{ per hour} = \$324$
Next, divide this total by Noah’s hourly rate to find the number of hours Noah would need to work:
$\$324 ÷ \$10.80 \text{ per hour} $ $ = 30 \text{ hours}$
Question 8 |
Diego’s current age is five times Martina’s age ten years ago. If Martina is currently $m$ years old, what is Diego’s current age in terms of $m$?
5$m$ | |
5$m$ − 10 | |
5$m$ − 50 | |
5$m$ + ($m$ − 10) | |
10($m$ − 5) |
Question 8 Explanation:
The correct answer is (C). Martina’s age ten years ago is:
$m − 10$
So Diego’s age is:
$5(m − 10)$
$= 5m − 50$
$m − 10$
So Diego’s age is:
$5(m − 10)$
$= 5m − 50$
Question 9 |
In a coordinate plane, triangle $ABC$ has coordinates: $(−2,7)$, $(−3,6)$, and $(4,5)$. If triangle $ABC$ is reflected over the $y$-axis, what are the coordinates of the new image?
$(−2,−7), (−3,−6), (−4,−5)$ | |
$(−2,−7), (−3,−6), (4,−5)$ | |
$(2,7), (3,6), (−4,5)$ | |
$(2,7), (3,6), (4,5)$ | |
$(2,−7), (3,−6), (−4,−5)$ |
Question 9 Explanation:
The correct answer is (C). One way to solve this problem is to draw the figure and then count how many units each point is from the $y$-axis, and to then count the same number of units in the opposite direction to find each point’s reflection. A more efficient method is to recognize that reflecting over the $y$-axis causes the $x$-value to switch sign and does not influence the $y$-value of the point.
Reflecting $(−2,7), (−3,6), (4,5)$ across the $y$-axis produces the points $(2,7), (3,6), (−4,5)$.
Reflecting $(−2,7), (−3,6), (4,5)$ across the $y$-axis produces the points $(2,7), (3,6), (−4,5)$.
Question 10 |
Arrange the following fractions in order from least to greatest.
$\dfrac{7}{5}, \dfrac{15}{4}, \dfrac{3}{2}, \dfrac{11}{4}, \dfrac{13}{3}$$\dfrac{7}{5}, \dfrac{15}{4}, \dfrac{3}{2}, \dfrac{11}{4}, \dfrac{13}{3}$ | |
$\dfrac{7}{5}, \dfrac{3}{2}, \dfrac{15}{4}, \dfrac{11}{4}, \dfrac{13}{3}$ | |
$\dfrac{7}{5}, \dfrac{3}{2}, \dfrac{11}{4}, \dfrac{15}{4}, \dfrac{13}{3}$ | |
$\dfrac{7}{5}, \dfrac{15}{4}, \dfrac{11}{4}, \dfrac{3}{2}, \dfrac{13}{3}$ | |
$\dfrac{3}{2}, \dfrac{7}{5}, \dfrac{11}{4}, \dfrac{15}{4}, \dfrac{13}{3}$ |
Question 10 Explanation:
The correct answer is (C). There are two useful methods for directly comparing the values of fractions: converting each fraction to a decimal and rewriting each fraction with a common denominator. In this case, the least common denominator would be 60 (5 ∗ 4 ∗ 3), and as a result, the optimal approach entails converting each fraction to a decimal, instead:
$\frac{7}{5} = 1.4$, $\frac{15}{4} = 3.75$, $\frac{3}{2} = 1.5$, $\frac{11}{4} = 2.75$, $\frac{13}{3} = 1.33$
Now, order the decimals from least to greatest, and match the resulting list with its corresponding list of fractions: $1.4, 1.5, 2.75, 3.75$, and $4.33$ which corresponds to:
$\dfrac{7}{5}, \dfrac{3}{2}, \dfrac{11}{4}, \dfrac{15}{4}, \dfrac{13}{3}$
$\frac{7}{5} = 1.4$, $\frac{15}{4} = 3.75$, $\frac{3}{2} = 1.5$, $\frac{11}{4} = 2.75$, $\frac{13}{3} = 1.33$
Now, order the decimals from least to greatest, and match the resulting list with its corresponding list of fractions: $1.4, 1.5, 2.75, 3.75$, and $4.33$ which corresponds to:
$\dfrac{7}{5}, \dfrac{3}{2}, \dfrac{11}{4}, \dfrac{15}{4}, \dfrac{13}{3}$
Question 11 |
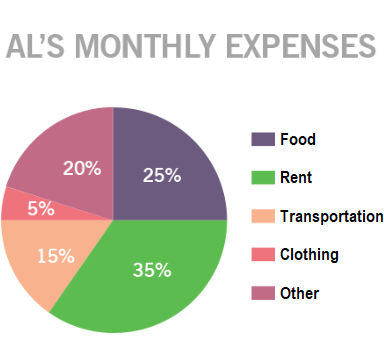
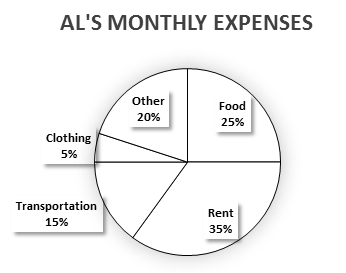
This pie chart shows Al’s monthly expenses. If Al spent a total of \$1,550 in one month, how much did he spend on clothes in that month?
\$77.50 | |
\$232.50 | |
\$775 | |
\$7.75 | |
\$1,627.50 |
Question 11 Explanation:
The correct answer is (A). Remember that $5\%$ is equivalent to $\frac{5}{100}$ or $.05$:
$.05 × \$1,550 = \$77.50$
$.05 × \$1,550 = \$77.50$
Question 12 |
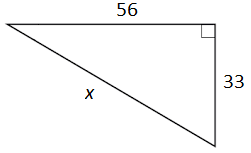
Calculate the value of $x$ for the right triangle shown below.
$66$ | |
$89$ | |
$56$ | |
$65$ | |
$75$ |
Question 12 Explanation:
The correct answer is (D). The Pythagorean theorem can be used to find a missing segment of a right triangle if two side lengths are given. The theorem relates the legs of a right triangle to its hypotenuse as $a^2 + b^2 = c^2$, where $a$ and $b$ are the legs and $c$ is the hypotenuse. The hypotenuse is the longest side in a right triangle and is always opposite the right angle.
Substitute the known values into their appropriate places and solve for the unknown side length:
$33^2 + 56^2 = c^2$
Evaluate the squares:
$1,089 + 3,136 = c^2$
$4,225 = c^2$
Evaluate the square root of both sides:
$\sqrt{c^2} = \sqrt{4,225}$
$c = 65$
Substitute the known values into their appropriate places and solve for the unknown side length:
$33^2 + 56^2 = c^2$
Evaluate the squares:
$1,089 + 3,136 = c^2$
$4,225 = c^2$
Evaluate the square root of both sides:
$\sqrt{c^2} = \sqrt{4,225}$
$c = 65$
Question 13 |
Oscar purchased a new hat that was on sale for $\$5.06$. The original price was $\$9.20$. What percentage discount was the sale price?
4.5% | |
41.4% | |
45% | |
55% | |
5.5% |
Question 13 Explanation:
The correct answer is (C). The percentage discount is the reduction in price divided by the original price. The difference between original price and sale price is:
$\$9.20 − \$5.06 = \$4.14$
The percentage discount is this difference divided by the original price:
$\$4.14 ÷ \$9.20 = 0.45$
Convert the decimal to a percentage by multiplying by 100%:
$0.45 × 100\% = 45\%$
$\$9.20 − \$5.06 = \$4.14$
The percentage discount is this difference divided by the original price:
$\$4.14 ÷ \$9.20 = 0.45$
Convert the decimal to a percentage by multiplying by 100%:
$0.45 × 100\% = 45\%$
Question 14 |
Anastasia needs to order liquid fertilizer for her landscaping company. She plans to keep the fertilizer in a large cylindrical storage tank, but isn’t sure how much it will hold. The tank is 10 feet tall and the circular base has a diameter of 10 feet. What is the volume of her storage tank?
78.5 ft³ | |
157 ft³ | |
3,140 ft³ | |
1,570 ft³ | |
785 ft³ |
Question 14 Explanation:
The correct answer is (E). The following is the formula for a cylinder:
Volume = (area of the base) (height)
The base of a cylinder is a circle, so you will also need the formula for the area of a circle, which is also provided on the formula sheet:
$\text{Area} = π(\text{radius})^2$
Combining these formulas, we get:
$V = πr^2h$
$V$ is volume, $r$ is the radius, and $h$ is the height of the cylinder. (Remember that the radius of a circle is half of the diameter.) Substitute the given values into the equation to solve for the volume:
$V = π \cdot (5)^2 \cdot 10$
$V = 250π$
Recall that $π$ (pi) is approximately equal to 3.14:
$250 \cdot 3.14 = 785$
Volume = (area of the base) (height)
The base of a cylinder is a circle, so you will also need the formula for the area of a circle, which is also provided on the formula sheet:
$\text{Area} = π(\text{radius})^2$
Combining these formulas, we get:
$V = πr^2h$
$V$ is volume, $r$ is the radius, and $h$ is the height of the cylinder. (Remember that the radius of a circle is half of the diameter.) Substitute the given values into the equation to solve for the volume:
$V = π \cdot (5)^2 \cdot 10$
$V = 250π$
Recall that $π$ (pi) is approximately equal to 3.14:
$250 \cdot 3.14 = 785$
Question 15 |
Kayla owns a house cleaning company and must give price quotes to potential customers. She determines her price by assuming a $\$25$ base charge and then adding $\$8$ for each bathroom and $\$4$ for every other room. If she uses $P$ to represent the price, $B$ to represent the bathrooms, and $R$ to represent the other rooms, which of the following defines her price quote formula?
$P = 25 + 12(BR)$ | |
$P = 25(4R + 8B)$ | |
$P = 25 + 8B + 4R$ | |
$P = (4)(8)(R + B) + 25$ | |
$P = (25 + 8B) + (25 + 4R)$ |
Question 15 Explanation:
The correct answer is (C). The price quote, $P$, will be equal to the total amount of charges. It’s given that there is a $\$25$ base charge, so we can begin by writing the price quote as $P = \$25$. To this base charge of $\$25$, $\$8$ per each bathroom, represented by the variable $B$, is added; our price quote is now $P = \$25 + \$8B$. Lastly, $\$4$ per each other room, $R$, is added, and the actual price quote is $P = \$25 + \$8B + \$4R$, or $P = 25 + 8B + 4R$.
Question 16 |
Use the information below to answer the question that follows.
A business recorded the number of customers who visited the store throughout the week. How many days had a number of visitors greater than the average number of visitors for the entire week?
$6$ days | |
$4$ days | |
$5$ days | |
$2$ days | |
$3$ days |
Question 16 Explanation:
The correct answer is (E). To answer the question we need to determine the average number of visitors for the week:
$\dfrac{13 + 12 + 16 + 19 + 25 + 33 + 22}{7}$ $= \dfrac{140}{7} = 20$
How many days had more than $20$ visitors?
Fri $= 25$
Sat $= 33$
Sun $= 22$
$3$ days exceeded the $20$-visitor average.
$\dfrac{13 + 12 + 16 + 19 + 25 + 33 + 22}{7}$ $= \dfrac{140}{7} = 20$
How many days had more than $20$ visitors?
Fri $= 25$
Sat $= 33$
Sun $= 22$
$3$ days exceeded the $20$-visitor average.
Question 17 |
In a factory there are two separate containers of stress balls. In the first container are $80$ balls, and in the second are $90$ balls. $40\%$ of the balls in the first container are defective, and $20\%$ in the second container are defective. In total, how many balls in the two containers are defective?
$102$ | |
$50$ | |
$60$ | |
$51$ |
Question 17 Explanation:
The correct answer is (B). Calculate the number of defective balls in each container and then add these two amounts:
$40\%$ of $80 = 0.40 \cdot 80 = 32$
$20\%$ of $90 = 0.20 \cdot 90 = 18$
$32 + 18 = 50$
$40\%$ of $80 = 0.40 \cdot 80 = 32$
$20\%$ of $90 = 0.20 \cdot 90 = 18$
$32 + 18 = 50$
Question 18 |
Which of the following fractions is greater than $0.4$ and less than $0.5$?
$\dfrac{6}{11}$ | |
$\dfrac{3}{10}$ | |
$\dfrac{12}{23}$ | |
$\dfrac{9}{20}$ |
Question 18 Explanation:
The correct answer is (D). Remember that $0.5$ is equivalent to $\frac{1}{2}$. Our fraction needs to be less than $\frac{1}{2}$.
Since $5.5$ is half of $11$, $\frac{6}{11}$ is greater than $\frac{1}{2}$. No good.
Since $11.5$ is half of $23$, $\frac{12}{23}$ is greater than $\frac{1}{2}$. No good.
This means our answer is either $\frac{3}{10}$ or ${9}{20}$.
$\frac{3}{10}$ is equivalent to $0.3$, which is less than $0.4$. No good.
$\frac{9}{20}$ must be correct. You could also solve by recognizing that $0.4 = \frac{4}{10} = \frac{8}{20}$ and $0.5 = \frac{5}{10} = \frac{10}{20}$, so $\frac{9}{20}$ works.
Since $5.5$ is half of $11$, $\frac{6}{11}$ is greater than $\frac{1}{2}$. No good.
Since $11.5$ is half of $23$, $\frac{12}{23}$ is greater than $\frac{1}{2}$. No good.
This means our answer is either $\frac{3}{10}$ or ${9}{20}$.
$\frac{3}{10}$ is equivalent to $0.3$, which is less than $0.4$. No good.
$\frac{9}{20}$ must be correct. You could also solve by recognizing that $0.4 = \frac{4}{10} = \frac{8}{20}$ and $0.5 = \frac{5}{10} = \frac{10}{20}$, so $\frac{9}{20}$ works.
Question 19 |
Use the menu below to answer the question that follows.
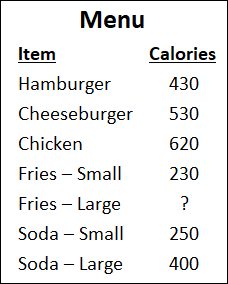Neil ordered the following for his family: two cheeseburgers, one hamburger, two large fries, one small fries, and three small sodas. If the total calories for the order is $3370$, what is the missing calorie information on the menu?
$1000$ | |
$400$ | |
$450$ | |
$480$ | |
$900$ |
Question 19 Explanation:
The correct answer is (C). Let's begin by totaling the calories for the items we are able to:
Two cheeseburgers $= 2 × 530 = 1,060$ calories
One hamburger $= 430$ calories
One small fries $= 230$ calories
Three small sodas $= 3 × 250 = 750$ calories
If we subtract each of the known calories from the total calories for the order we will know how many calories came from two large fries:
$3,370 − 1,060 − 430 − 230 − 750 = 900$
$900$ calories came from two orders of large fries. Each order of fries is $450$ calories.
Two cheeseburgers $= 2 × 530 = 1,060$ calories
One hamburger $= 430$ calories
One small fries $= 230$ calories
Three small sodas $= 3 × 250 = 750$ calories
If we subtract each of the known calories from the total calories for the order we will know how many calories came from two large fries:
$3,370 − 1,060 − 430 − 230 − 750 = 900$
$900$ calories came from two orders of large fries. Each order of fries is $450$ calories.
Question 20 |
Aisha wants to paint the walls of a room. She knows that each can of paint contains one gallon. A half gallon will completely cover a $55$ square feet of wall. Each of the four walls of the room is $10$ feet high. Two of the walls are $10$ feet wide and two of the walls are $15$ feet wide. How many $1$-gallon buckets of paint does Aisha need to buy in order to fully paint the room?
$4$ | |
$5$ | |
$9$ | |
$10$ | |
$15$ |
Question 20 Explanation:
The correct answer is (B). The total number of buckets necessary will be the total area of the walls divided by the total area covered by each bucket. First, calculate the area of the walls Aisha wants to paint. Two of the walls are $10 × 10$ and two of the walls are $10 × 15$:
$2 (10 × 10) = 200$ sq. ft. $2 (10 × 15) = 300$ sq. ft. So the total square footage of the walls is $500$. If a half gallon of paint will cover $55$ square feet, then each gallon will cover $2 × 55 = 110$ square feet. Four gallons can only cover $440$ square feet. Five gallons will cover $550$ square feet, which will be enough for the entire area of the walls.
$2 (10 × 10) = 200$ sq. ft. $2 (10 × 15) = 300$ sq. ft. So the total square footage of the walls is $500$. If a half gallon of paint will cover $55$ square feet, then each gallon will cover $2 × 55 = 110$ square feet. Four gallons can only cover $440$ square feet. Five gallons will cover $550$ square feet, which will be enough for the entire area of the walls.
Question 21 |
The data in the table below shows the results of Tracy trying to train her dog Snowy.
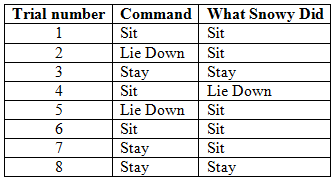In what percentage of these trials did Snowy obey the command given?
25% | |
37.5% | |
50% | |
62.5% | |
75% |
Question 21 Explanation:
The correct answer is (C). Calculate the percentage of trials that Snowy obeyed by dividing the number of times Snowy obeyed by the total number of commands given. The trials in which Snowy obeyed: trial 1, trial 3, trial 6, trial 8, which sums to 4 trials. There are 8 total trials so the percentage is:
$\dfrac{4}{8}$ $= \dfrac{1}{2} = 50\%$
$\dfrac{4}{8}$ $= \dfrac{1}{2} = 50\%$
Question 22 |
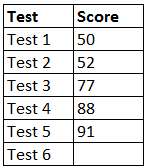
Max struggled with his math class early in the year, but he has been working hard to improve his scores. There is one test left, and he is hoping that his final average test score will be 75. What score will he need to get on Test 6 to finish the year with an average score of 75?
75 | |
85 | |
92 | |
98 | |
100 |
Question 22 Explanation:
The correct answer is (C). The average of a set of data points is the sum of the data points divided by the total number of data points. In this case, we are given 5 out of 6 data points, the number of data points, and the desired average. Substitute the given values into the formula for the average, using a variable to represent the unknown test score, and then solve for the variable:
Average = sum of data points ÷ number of data points
$75 = (50 + 52 + 77 + 88 + 91 + x) ÷ 6$
Now solve for $x$. Start with the addition:
$75 = (358 + x) ÷ 6$
Next, eliminate the denominator by multiplying both sides by 6:
$450 = 358 + x$
The last step is to subtract 358 from both sides:
$x = 92$
Average = sum of data points ÷ number of data points
$75 = (50 + 52 + 77 + 88 + 91 + x) ÷ 6$
Now solve for $x$. Start with the addition:
$75 = (358 + x) ÷ 6$
Next, eliminate the denominator by multiplying both sides by 6:
$450 = 358 + x$
The last step is to subtract 358 from both sides:
$x = 92$
Question 23 |
A student is calculating the average of a list of seven numbers. After adding the seven numbers together, he accidentally multiplied by 7 instead of dividing and got 392. What could the student do to get the correct average without having to clear the calculator and start over?
Divide the incorrect result by 7 | |
Divide the incorrect result by 49 | |
Multiply the incorrect result by 7 | |
Divide the incorrect result by 14 | |
Divide the incorrect result by 77 |
Question 23 Explanation:
The correct answer is (B). Let $x$ equal the sum of the seven numbers. The student should have divided $x$ by 7 to get the average, giving the correct result of $\frac{x}{7}$. Since they accidentally multiplied by 7, the calculator shows 7$x$.
To get the correct answer, the student needs to divide by 7 twice, which is the same as dividing by 49:
$\dfrac{7x}{49} = \dfrac{x}{7}$
To get the correct answer, the student needs to divide by 7 twice, which is the same as dividing by 49:
$\dfrac{7x}{49} = \dfrac{x}{7}$
Question 24 |
List A consists of the numbers ${2, 9, 5, 1, 13}$, and list B consists of the numbers ${7, 4, 12, 15, 18}$.
If the two lists are combined, what is the median of the combined list?5 | |
6 | |
7 | |
8 | |
9 |
Question 24 Explanation:
The correct answer is (D). Recall that the median of a set of data is the value located in the middle of the data set. In the case of a data set that contains an even number of numbers, the median is the average of the two middle numbers. Combine the 2 sets provided, and organize them in ascending order:
${1, 2, 4, 5, 7, 9, 12, 13, 15, 18}$
Since there are an even number of items in the resulting list, the median is the average of the two middle numbers.
Median $= (7 + 9) ÷ 2 = 8$
${1, 2, 4, 5, 7, 9, 12, 13, 15, 18}$
Since there are an even number of items in the resulting list, the median is the average of the two middle numbers.
Median $= (7 + 9) ÷ 2 = 8$
Question 25 |
Tavon's flight is 270 minutes long. How many hours does the flight last?
$4$ hours | |
$4 \frac{1}{2}$ hours | |
$5$ hours | |
$5 \frac{1}{2}$ hours |
Question 25 Explanation:
The correct answer is (B).
$\require{cancel} 270 \cancel{\text{minutes}} \cdot \dfrac{1 \text{ hour}}{60 \cancel{\text{minutes}}}$ $= \dfrac{270}{60} \text{ hours}$ $= \dfrac{27}{6} \text{hours}$
$\dfrac{27}{6} = \dfrac{9}{2} = 4 \dfrac{1}{2}$
$\require{cancel} 270 \cancel{\text{minutes}} \cdot \dfrac{1 \text{ hour}}{60 \cancel{\text{minutes}}}$ $= \dfrac{270}{60} \text{ hours}$ $= \dfrac{27}{6} \text{hours}$
$\dfrac{27}{6} = \dfrac{9}{2} = 4 \dfrac{1}{2}$
Question 26 |
$6.6 × 10^{−4}$
0.000066 | |
0.00066 | |
0.0066 | |
0.066 | |
0.66 |
Question 26 Explanation:
The correct answer is (B). Multiplying a decimal value by 10 raised to a power is equivalent to moving the decimal point to the left or right the number of times indicated by the power.
In the case of a negative exponent, the decimal is moved to the left (this is the same as dividing by 10 a number of times).
In the case of a positive exponent, the decimal is moved to the right (this is the same as multiplying by 10 a number of times).
The negative exponent here, −4, indicates that the decimal point is to be moved to the left 4 places:
$6.6 × 10^{−4} = 0.66 × 10^{−3}$
$= 0.066 × 10^{−2}$
$= 0.0066 × 10^{−1}$
$= 0.00066 × 10^{0}$
$= 0.00066$
In the case of a negative exponent, the decimal is moved to the left (this is the same as dividing by 10 a number of times).
In the case of a positive exponent, the decimal is moved to the right (this is the same as multiplying by 10 a number of times).
The negative exponent here, −4, indicates that the decimal point is to be moved to the left 4 places:
$6.6 × 10^{−4} = 0.66 × 10^{−3}$
$= 0.066 × 10^{−2}$
$= 0.0066 × 10^{−1}$
$= 0.00066 × 10^{0}$
$= 0.00066$
Question 27 |
$ABC$ is a triangle with coordinates $(3, 1),$ $(6, 1),$ and $(1, 3)$. It is translated to points $A′(−3, 3),$ $B′( 0, 3),$ and $C′(−5, 5)$. Find the rule for the translation.
6 units right and 2 units down | |
2 units left and 6 units up | |
6 units down and 2 units right | |
6 units left and 2 units up | |
2 units left and 6 units right |
Question 27 Explanation:
The correct answer is (D). The rule of translation is the rule, which when applied to the first set of points, yields the second set of points. The difference between the $x$ values of the non-translated and translated points is:
$(x_2 − x_1) = (−3 − 3) $ $ = (0 − 6) = (−5 − 1) = −6$
This corresponds to a shift of 6 units to the left.
Likewise, for the $y$ values:
$(y_2 − y_1) = (3 − 1) $ $ = (3 − 1) = (5 − 3) = 2$
This corresponds to a vertical shift of 2 units.
$(x_2 − x_1) = (−3 − 3) $ $ = (0 − 6) = (−5 − 1) = −6$
This corresponds to a shift of 6 units to the left.
Likewise, for the $y$ values:
$(y_2 − y_1) = (3 − 1) $ $ = (3 − 1) = (5 − 3) = 2$
This corresponds to a vertical shift of 2 units.
Question 28 |
There are 5 blue marbles, 4 red marbles, and 3 yellow marbles in a box. If Isabella randomly selects a marble from the box, what is the probability of her selecting a red or yellow marble?
$\dfrac{1}{4}$ | |
$\dfrac{1}{3}$ | |
$\dfrac{7}{12}$ | |
$\dfrac{3}{4}$ | |
$\dfrac{2}{3}$ |
Question 28 Explanation:
The correct answer is (C). A probability is the likelihood of a successful event occurring divided by the total number of events possible. In this case, a successful event is selecting either a red or a yellow marble and the total number of events possible is the total number of marbles.
Number of red and yellow marbles: $4 + 3 = 7$
Total number of marbles: $5 + 4 + 3 = 12$
Probability: $\dfrac{7}{12}$
Number of red and yellow marbles: $4 + 3 = 7$
Total number of marbles: $5 + 4 + 3 = 12$
Probability: $\dfrac{7}{12}$
Question 29 |
A river rafting guide offers group trips. She charges \$250 for 2 people and \$40 more for each additional person. If 5 friends share the cost of a trip equally, how much will each person pay?
\$40 | |
\$58 | |
\$74 | |
\$90 | |
\$370 |
Question 29 Explanation:
The correct answer is (C). First calculate the entire cost of the trip. Start with \$250 for the first two people and then add \$40 for each of the other three:
$250 + 40 + 40 + 40 = \$370$
Then divide this amount by 5 to determine the amount that each person will pay:
$\$370 ÷ 5 = \$74$
$250 + 40 + 40 + 40 = \$370$
Then divide this amount by 5 to determine the amount that each person will pay:
$\$370 ÷ 5 = \$74$
Question 30 |
Consider the list:
$2, 2, 3, 5, 9, 11, 17, 21$ If the number $23$ is added to the list, which measurement will NOT change?Mean | |
Median | |
Mode | |
Range | |
Average |
Question 30 Explanation:
The correct answer is (C). The mode will not change. The mode is the number that appears the most frequently; in this case it is $2$. The remaining measures will change:
The mean is the average, and in this case, it will increase because a number larger than the current average is added to the list.
The median is the number in the middle, and it will change from $7$ to $9$.
The range is the difference between the highest and lowest numbers and will change from $19$ to $21$ because a new maximum value is added to the list ($21 − 2 = 19$ and $23 − 2 = 21$).
The mean is the average, and in this case, it will increase because a number larger than the current average is added to the list.
The median is the number in the middle, and it will change from $7$ to $9$.
The range is the difference between the highest and lowest numbers and will change from $19$ to $21$ because a new maximum value is added to the list ($21 − 2 = 19$ and $23 − 2 = 21$).
Question 31 |
The points represented by the $(x, y)$ coordinate pairs in the table below all lie on line $k$.
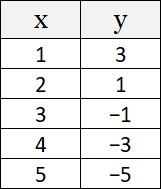What is the slope of line $k$?
−5 | |
−3 | |
−2 | |
2 | |
5 |
Question 31 Explanation:
The correct answer is (C). We are told that all the points lie on line $k$. Therefore, we can calculate the slope as the change in $y$ divided by the change in $x$ using any two of the points. Using points $(1, 3)$ and $(5, −5)$ the slope is calculated as follows:
Slope $= \dfrac{y_2 − y_1}{x_2 − x_1}$
Slope $= \dfrac{−5 − 3}{5 − 1}$
Slope $= \dfrac{−8}{4}$
Slope $= −2$
Slope $= \dfrac{y_2 − y_1}{x_2 − x_1}$
Slope $= \dfrac{−5 − 3}{5 − 1}$
Slope $= \dfrac{−8}{4}$
Slope $= −2$
Question 32 |
$\$126$ | |
$\$250$ | |
$\$325$ | |
$\$350$ | |
$\$325$ |
Question 32 Explanation:
The correct answer is (D). One method for solving this problem is to recognize that the ratio of the amount Al spends on food to the amount he spends on transportation will equal the ratio of the percentage of his income spent on food to the percentage spent on transportation. Expressed mathematically:
$\dfrac{\text{Amount spent on food}}{\text{Amount spent on transportation}}$
$= \dfrac{\text{Percentage spent on food}}{\text{Percentage spent on transportation}}$
Substitute the known values to then solve for the unknown amount spent on food:
$\dfrac{\text{Amount spent on food}}{\$210} = \dfrac{25}{15}$
Cross multiply and simplify to solve:
Amount spent on food $= \dfrac{\$210 \cdot 25}{15} = \$350$
$\dfrac{\text{Amount spent on food}}{\text{Amount spent on transportation}}$
$= \dfrac{\text{Percentage spent on food}}{\text{Percentage spent on transportation}}$
Substitute the known values to then solve for the unknown amount spent on food:
$\dfrac{\text{Amount spent on food}}{\$210} = \dfrac{25}{15}$
Cross multiply and simplify to solve:
Amount spent on food $= \dfrac{\$210 \cdot 25}{15} = \$350$
Question 33 |
A teacher creates a final exam with 75 questions and expects it to take 90 minutes to complete. The exam consists of 19 short-answer questions with the remainder of the questions being multiple choice. How much time does the teacher expect his students to spend on each of the multiple choice questions?
Which single piece of information is necessary to solve the problem above?
The number of multiple choice questions | |
The time the teacher expects each short-answer question to take | |
The percentage of questions that are multiple choice | |
The number of students taking the exam | |
The average time the teacher expects each question on the exam to take |
Question 33 Explanation:
The correct answer is (B). Since there are 75 questions on the exam and 19 of the questions are short-answer, we can determine that there are 56 multiple choice questions.
Let $a$ = average time required for each multiple choice question.
Let $b$ = average time required for each short-answer question.
Since the exam is expected to take a total of 90 minutes:
$a(56) + b(19) = 90$
If we are given $b$, the time required for each short-answer question, we can use the above equation to solve for $a$, the time required for each multiple choice question.
Let $a$ = average time required for each multiple choice question.
Let $b$ = average time required for each short-answer question.
Since the exam is expected to take a total of 90 minutes:
$a(56) + b(19) = 90$
If we are given $b$, the time required for each short-answer question, we can use the above equation to solve for $a$, the time required for each multiple choice question.
Question 34 |
Susan, Gus, Harold, and Jeff were left an inheritance by their grandfather. If Susan receives $\frac{5}{16}$ of the inheritance, Gus receives $\frac{1}{8}$ of the inheritance, Harold receives $\frac{3}{16}$ of the inheritance, and Jeff receives the remainder, what fraction of the inheritance does Jeff receive?
$\dfrac{5}{16}$ | |
$\dfrac{7}{16}$ | |
$\dfrac{3}{8}$ | |
$\dfrac{1}{8}$ | |
$\dfrac{5}{8}$ |
Question 34 Explanation:
The correct answer is (C). Since the inheritance is shared between the four grandchildren, the total of their fractions must sum to 1 (whole).
Susan’s Fraction + Gus’ Fraction + Harold’s Fraction + Jeff’s Fraction = 1
$s+g+h+j=1$
$\dfrac{5}{16}+\dfrac{1}{8}+\dfrac{3}{16}+j=1$
$j=1-\dfrac{5}{16}-\dfrac{1}{8}-\dfrac{3}{16}$
When adding or subtracting fractions we need a common denominator (least common multiple) which is 16 in this case.
$j = \dfrac{16}{16}-\dfrac{5}{16}-\dfrac{2}{16}-\dfrac{3}{16}$
$j = \dfrac{16}{16}-\dfrac{10}{16}$
$j=\dfrac{6}{16}$
$j=\dfrac{3}{8}$
Susan’s Fraction + Gus’ Fraction + Harold’s Fraction + Jeff’s Fraction = 1
$s+g+h+j=1$
$\dfrac{5}{16}+\dfrac{1}{8}+\dfrac{3}{16}+j=1$
$j=1-\dfrac{5}{16}-\dfrac{1}{8}-\dfrac{3}{16}$
When adding or subtracting fractions we need a common denominator (least common multiple) which is 16 in this case.
$j = \dfrac{16}{16}-\dfrac{5}{16}-\dfrac{2}{16}-\dfrac{3}{16}$
$j = \dfrac{16}{16}-\dfrac{10}{16}$
$j=\dfrac{6}{16}$
$j=\dfrac{3}{8}$
Question 35 |
A manufacturer packages their high-quality pencils in packs that hold 15 pencils. There are 281 pencils left to be packed. How many complete packs can be filled.
18 | |
20 | |
16 | |
17 | |
19 |
Question 35 Explanation:
The correct answer is (A). We need to determine how many packs of 15 can be completed with 281 pencils. In other words, how many times does 15 “go into” 281?
The simplest way to tackle this is to use the calculator provided on the test.
$\dfrac{281}{15}= 18.73$
We are able to complete 18 complete packs and 0.73 of the 19th pack.
The question specifically asks for the number of complete packs, so the correct answer is 18 packs.
The simplest way to tackle this is to use the calculator provided on the test.
$\dfrac{281}{15}= 18.73$
We are able to complete 18 complete packs and 0.73 of the 19th pack.
The question specifically asks for the number of complete packs, so the correct answer is 18 packs.
Question 36 |
Tim is in the process of painting a large mural on the side of a building. The mural was 28% complete before Tim began working on it today. Today, after spending 4 hours on the mural, it is now 40% complete. If he continues progressing at the same rate, how many more hours will be needed to complete the mural?
16 hours | |
12 hours | |
10 hours | |
24 hours | |
20 hours |
Question 36 Explanation:
The correct answer is (E). Since 28% of the mural was already painted and Tim brought the mural to 40% painted, he must have painted 40% − 28% = 12% of the mural today.
It took him 4 hours to paint that 12% portion.
60% of the mural remains to be painted. How many hours will this require?
To find out we can set up an equivalent proportion:
$\dfrac{4 \text{ hours}}{12\%}=\dfrac{x \text{ hours}}{60\%}$
$(4)(60) = (12)(x)$
$240 = 12x$
$x=\dfrac{240}{12}$
$x = 20$
It will take 20 hours to complete the mural.
(Note: You might also solve by noticing that 12% goes into 60% five times, and 5 × 4 hours = 20 hours.)
It took him 4 hours to paint that 12% portion.
60% of the mural remains to be painted. How many hours will this require?
To find out we can set up an equivalent proportion:
$\dfrac{4 \text{ hours}}{12\%}=\dfrac{x \text{ hours}}{60\%}$
$(4)(60) = (12)(x)$
$240 = 12x$
$x=\dfrac{240}{12}$
$x = 20$
It will take 20 hours to complete the mural.
(Note: You might also solve by noticing that 12% goes into 60% five times, and 5 × 4 hours = 20 hours.)
Question 37 |
A university gave 2 Bachelor of Science (BS) degrees for every 7 Bachelor of Arts (BA) degrees. If the combined total number of BS and BA degrees was 6,327, how many Bachelor of Science degrees were given?
1406 | |
1808 | |
1346 | |
1039 | |
703 |
Question 37 Explanation:
The correct answer is (A). If 2 BS degrees are given for every 7 BA degrees, it means that 2 BS degrees are given for every 9 Bachelor degrees in total.
This means that 2 out of 9 of the degrees was a BS degree. We need to determine what $\frac{2}{9}$ of 6,327 is.
$\dfrac{2}{9}*6372=1406$
1406 of the Bachelor degrees given were a Bachelor of Science degree.
This means that 2 out of 9 of the degrees was a BS degree. We need to determine what $\frac{2}{9}$ of 6,327 is.
$\dfrac{2}{9}*6372=1406$
1406 of the Bachelor degrees given were a Bachelor of Science degree.
Question 38 |
Doug and Heidi work at the same clinic. They are both scheduled to work on January 1st. If Doug is scheduled to work every 3 days (1st, 4th, 7th, ...) and Heidi is scheduled to work every 5 days (1st, 6th, 11th, ...), including Jan 1st, how many times will they work together over the course of 56 days?
3 | |
6 | |
4 | |
5 | |
2 |
Question 38 Explanation:
The correct answer is (C). A great way to tackle this problem is to recognize that their work days will align every 15 days because 15 is the least common multiple of 3 and 5.
Day 1, 16, 31, 46 are the four days when they will work on the same day.
Another approach would be to list out the days each will be working and look for the days that the two lists have in common (underlined):
Doug: 1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, 40, 43, 46, 49, 52, 55
Heidi: 1, 6, 11, 16, 21, 26, 31, 36, 41, 46, 51, 56
They will work 4 days together.
Day 1, 16, 31, 46 are the four days when they will work on the same day.
Another approach would be to list out the days each will be working and look for the days that the two lists have in common (underlined):
Doug: 1, 4, 7, 10, 13, 16, 19, 22, 25, 28, 31, 34, 37, 40, 43, 46, 49, 52, 55
Heidi: 1, 6, 11, 16, 21, 26, 31, 36, 41, 46, 51, 56
They will work 4 days together.
Question 39 |
A bicycle manufacturer makes two models of bikes: “mountain” and “beach.” In their warehouse this morning they had 2,112 total bicycles, and 7 out of every 12 of those bikes was a “mountain” model. After shipping 75 “beach” models from the warehouse, how many “beach” model bikes will remain?
978 | |
1,157 | |
880 | |
671 | |
805 |
Question 39 Explanation:
The correct answer is (E). If “7 out of every 12” bikes is a “mountain” bike, then 5 out of every 12 bikes must be a “beach” bike.
Number of “beach” bikes initially $= \dfrac{5}{12}*2{,}112=880$
After shipping 75 bikes how many will remain?
Number of “beach” bikes remaining $= 880 − 75 = 805$
Number of “beach” bikes initially $= \dfrac{5}{12}*2{,}112=880$
After shipping 75 bikes how many will remain?
Number of “beach” bikes remaining $= 880 − 75 = 805$
Question 40 |
Aiden’s new toy car is a 1/64th model of the actual car, meaning a feature measuring 1 mm on his toy would be 64 mm on the actual car. He measures the wheel base on his toy and gets 44 mm. What would be the expected wheelbase of the actual car in meters?
2.8m | |
4.1m | |
6.9m | |
4.8m | |
7.5m |
Question 40 Explanation:
The correct answer is (A). To solve, we can set up an equivalent proportion:
$ \dfrac{1\text{ mm}}{64\text{ mm}}=\dfrac{44\text{ mm}}{x\text{ mm}}$
Cross multiplying:
$(1)(x) = (64)(44) $
$x = 2816 \text{ mm}$
To convert millimeters to meters, we divide by 1000:
$\dfrac{2816}{1000} = 2.816 \approx 2.8 \text{ m}$
$ \dfrac{1\text{ mm}}{64\text{ mm}}=\dfrac{44\text{ mm}}{x\text{ mm}}$
Cross multiplying:
$(1)(x) = (64)(44) $
$x = 2816 \text{ mm}$
To convert millimeters to meters, we divide by 1000:
$\dfrac{2816}{1000} = 2.816 \approx 2.8 \text{ m}$
Question 41 |
What is the least common multiple of 105 and 231?
4,179 | |
2,310 | |
1,155 | |
24,255 | |
495 |
Question 41 Explanation:
The correct answer is (C). With these types of questions you should start by fully factoring each number so that it is expressed as a product of primes. The typical approach is to use a factor tree:
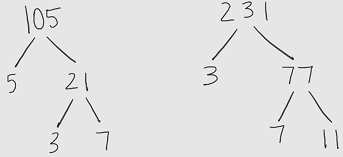
Next, list the prime factors of each number:
Prime factors of 105: 3, 5, 7
Prime factors of 231: 3, 7, 11
Combine the lists, but do not duplicate any factor that appears in both lists: Prime factors without duplicate factors: 3, 5, 7, 11
(Notice that 3 and 7 are only listed once since they appear in the factor trees of both numbers.)
Find the product of the numbers:
3 ∗ 5 ∗ 7 ∗ 11 = 1, 155
The least common multiple is 1,155.
Because this question is multiple choice, we could instead work backwards from the answers.
We check each answer choice to see whether or not it can be divided by 105 and by 231:
4,179 – NO
2,310 – YES
1,155 – YES
24,255 – YES
495 – NO
We then choose the multiple that is the least. In this case 1,155 is the least multiple of each number (it is the smallest number that can be divided by both 105 and 231).
Next, list the prime factors of each number:
Prime factors of 105: 3, 5, 7
Prime factors of 231: 3, 7, 11
Combine the lists, but do not duplicate any factor that appears in both lists: Prime factors without duplicate factors: 3, 5, 7, 11
(Notice that 3 and 7 are only listed once since they appear in the factor trees of both numbers.)
Find the product of the numbers:
3 ∗ 5 ∗ 7 ∗ 11 = 1, 155
The least common multiple is 1,155.
Because this question is multiple choice, we could instead work backwards from the answers.
We check each answer choice to see whether or not it can be divided by 105 and by 231:
4,179 – NO
2,310 – YES
1,155 – YES
24,255 – YES
495 – NO
We then choose the multiple that is the least. In this case 1,155 is the least multiple of each number (it is the smallest number that can be divided by both 105 and 231).
Question 42 |
A bag contains only green and red balls. A player draws a single ball from the bag. If the ball is green they win, and if it is red they lose. Initially, the bag contained 20 green balls and an unknown (non-zero) number of red balls.
When 24 additional green balls are added to the bag with no change to the number of red balls, it causes the probability of losing to be halved (i.e. a player is now half as likely to lose).
How many red balls are in the bag?
5 | |
6 | |
4 | |
8 | |
12 |
Question 42 Explanation:
The correct answer is (C) Let $r$ represent the number of red balls and $g$ the number of green balls originally in the bag. Let total be the total number of balls originally in the bag (= $r$ + $g$).
The probability of losing can be expressed as:
$\text{P(Losing)} = \dfrac {r}{r+g} = \dfrac{r}{\text{total}}$
“Logical” Approach:
We are told that when the number of green balls was increased by 24 without changing the number of red balls, the probability of losing was halved. Put another way, when total was increased by 24, the probability of losing was halved.
But, for the probability of losing to be halved, the total must have been doubled (since we know that the number of red balls did not change).
Adding 24 balls doubled the total, therefore there must have been 24 balls in the bag originally.
And if 20 of the 24 original balls was green, the balance of 4 must have been red.
Algebraic Approach:
$P\text{(Losing originally)} = \dfrac {r}{r+g} $ $ = \dfrac {r}{r+20}$
$P\text{(Losing after adding 24 more green balls)}$
$= \dfrac {r}{r+20+24} = \dfrac {r}{r+44}$
We also know that:
$P\text{(Losing after adding 24 more green balls)}$
$= \dfrac {1}{2} \ast P\text{(Losing originally)}$
Which means that:
$2 \ast P\text{(Losing after adding 24 more green balls)}$
$= P\text{(Losing originally)}$
$2*\dfrac {r}{r+44}=\dfrac {r}{r+20}$
$\dfrac {2r}{r+44}=\dfrac {r}{r+20}$
Cross multiplying:
$(2r)(r + 20) = (r + 44)(r)$
Dividing both sides by $r$:
$(2)(r + 20) = (r + 44)$
$2r + 40 = r + 44$
$r = 4$
The probability of losing can be expressed as:
$\text{P(Losing)} = \dfrac {r}{r+g} = \dfrac{r}{\text{total}}$
“Logical” Approach:
We are told that when the number of green balls was increased by 24 without changing the number of red balls, the probability of losing was halved. Put another way, when total was increased by 24, the probability of losing was halved.
But, for the probability of losing to be halved, the total must have been doubled (since we know that the number of red balls did not change).
Adding 24 balls doubled the total, therefore there must have been 24 balls in the bag originally.
And if 20 of the 24 original balls was green, the balance of 4 must have been red.
Algebraic Approach:
$P\text{(Losing originally)} = \dfrac {r}{r+g} $ $ = \dfrac {r}{r+20}$
$P\text{(Losing after adding 24 more green balls)}$
$= \dfrac {r}{r+20+24} = \dfrac {r}{r+44}$
We also know that:
$P\text{(Losing after adding 24 more green balls)}$
$= \dfrac {1}{2} \ast P\text{(Losing originally)}$
Which means that:
$2 \ast P\text{(Losing after adding 24 more green balls)}$
$= P\text{(Losing originally)}$
$2*\dfrac {r}{r+44}=\dfrac {r}{r+20}$
$\dfrac {2r}{r+44}=\dfrac {r}{r+20}$
Cross multiplying:
$(2r)(r + 20) = (r + 44)(r)$
Dividing both sides by $r$:
$(2)(r + 20) = (r + 44)$
$2r + 40 = r + 44$
$r = 4$
Question 43 |
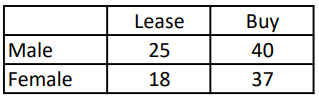
The table below shows the distribution of attendees of a conference by sex and by whether they leased or bought the car they drive.
Among those attendees who lease their car, what percentage are female?
Among those attendees who lease their car, what percentage are female?
41.9% | |
15.0% | |
72.0% | |
48.6% | |
32.7% |
Question 43 Explanation:
The correct answer is (A). It is crucial to pay close attention to the wording of the question any time you have a two-way table question such as this.
Notice that we are NOT being asked the percentage of attendees that are both female and lease their car.
Instead, we are told to only look “among those attendees who lease their car.”
There are a total of 43 (= 25 + 18) attendees who lease their car.
18 of these 43 are female.
Thus, among those attendees who lease their car, the percentage that are female. is:
$ \dfrac{18}{43} \approx 0.419 = 41.9\%$
Notice that we are NOT being asked the percentage of attendees that are both female and lease their car.
Instead, we are told to only look “among those attendees who lease their car.”
There are a total of 43 (= 25 + 18) attendees who lease their car.
18 of these 43 are female.
Thus, among those attendees who lease their car, the percentage that are female. is:
$ \dfrac{18}{43} \approx 0.419 = 41.9\%$
Question 44 |
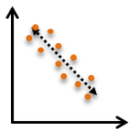
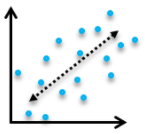
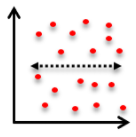
Which of the following scatter plots shows a weak negative correlation between $x$ and $y$?
 | |
 | |
 | |
 | |
 |
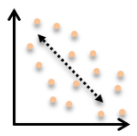Question 44 Explanation:
The correct answer is (E). The points in this scatter plot show a trend along a line of negative slope, but the points are not particularly tightly grouped around the line, making it a “weak negative correlation.”
Answer choice (A) also has a negative slope, but here the points are tightly grouped about the line, making it a “strong negative correlation.”
Answer choice (A) also has a negative slope, but here the points are tightly grouped about the line, making it a “strong negative correlation.”
Question 45 |
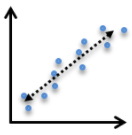
A company is analyzing data which shows the relationship between the hourly wage of employees (W) and the number of vacation days taken (D). Which statement below best describes the relationship between W and D?
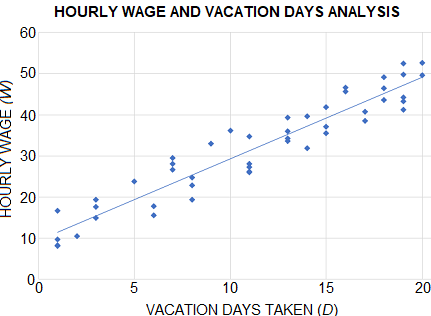
An increase in W causes an increase in D | |
There is no correlation between W and D | |
There is a positive correlation between W and D | |
There is a negative correlation between W and D | |
An increase in D causes an increase in W |
Question 45 Explanation:
The correct answer is (C). Correlation does not imply causation. A graph like this one shows a clear, positive correlation between two variables—meaning as D increases, W also tends to increase.
However, just because there is a positive correlation, we cannot assume that either variable causes a change in the other variable.
However, just because there is a positive correlation, we cannot assume that either variable causes a change in the other variable.
Question 46 |
The scatter plot below shows data points along with a line of best fit. Which of the following is the equation for the graph of the line of best fit?
−10$x$ + 10 | |
10$x$ + 9 | |
2$x$ + 10 | |
5$x$ + 10 | |
−5$x$ − 9 |
Question 46 Explanation:
The correct answer is (C). The line has a positive slope (it goes up as you move from left to right). This means the correct answer is one with a positive slope: (B), (C), or (D).
To determine the slope look at the change in $y$ relative to the change in $x$. It appears that the $y$-value of the graph increases by 10 hours as the $x$-value increases by 5 days.
$\text{slope} = m = \dfrac{\text{Change in } y}{\text{Change in } x}$
$m = \dfrac{10}{5} = 2$
Recall that the slope-intercept form of a line is: $y = mx + b$
Only answer choice (C) has a line with a slope of $m$ = 2.
To determine the slope look at the change in $y$ relative to the change in $x$. It appears that the $y$-value of the graph increases by 10 hours as the $x$-value increases by 5 days.
$\text{slope} = m = \dfrac{\text{Change in } y}{\text{Change in } x}$
$m = \dfrac{10}{5} = 2$
Recall that the slope-intercept form of a line is: $y = mx + b$
Only answer choice (C) has a line with a slope of $m$ = 2.
Question 47 |
The pictograph below shows bicycle sales by category in the USA for 2017. According to the pictograph, what was the mean sales amongst the three categories of bicycles?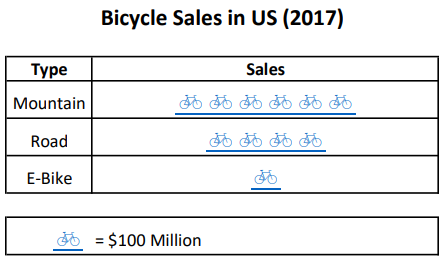
$3.7 Million | |
$400 Million | |
$37 Million | |
$4.0 Million | |
$370 Million |
Question 47 Explanation:
The correct answer is (E). According to the bottom of the pictograph, each bicycle icon represents \$100 Million in sales.
This means there were:
6 × \$100 = \$600 Million in Mountain bike sales.
4 × \$100 = \$400 Million in Road bike sales.
1 × \$100 = \$100 Million in Electric bike sales.
The sum of these sales figures for the 3 categories:
\$600 + \$400 + \$100 Million = \$1100 Million
To find the mean we need to divide by the “number of numbers”:
$\text{Mean} = \dfrac{\$1100 \text{ Million}}{3}$
$\text{Mean} = \$366.6 \text{ Million}$
\$370 Million is the best answer.
This means there were:
6 × \$100 = \$600 Million in Mountain bike sales.
4 × \$100 = \$400 Million in Road bike sales.
1 × \$100 = \$100 Million in Electric bike sales.
The sum of these sales figures for the 3 categories:
\$600 + \$400 + \$100 Million = \$1100 Million
To find the mean we need to divide by the “number of numbers”:
$\text{Mean} = \dfrac{\$1100 \text{ Million}}{3}$
$\text{Mean} = \$366.6 \text{ Million}$
\$370 Million is the best answer.
Question 48 |
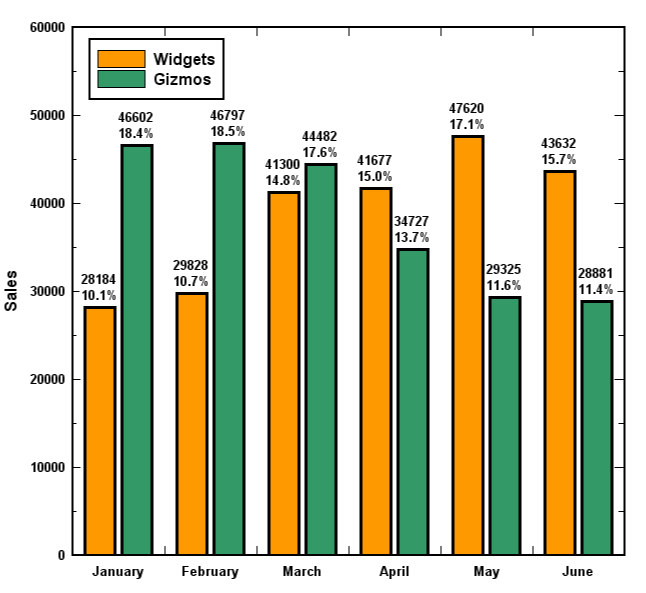
The graph below shows data for two products, Widgets and Gizmos. For each product the graph shows the sales in units sold and the sales as a percentage of total company sales. For the data shown, what was the greatest decrease in Gizmos unit sales experienced from one month to the next (consecutive months)?
7382 | |
1209 | |
8279 | |
3730 | |
9755 |
Question 48 Explanation:
The correct answer is (E). The Gizmos sales are shown in green.
We can visually deduce that the greatest decrease in Gizmos unit sales in consecutive months occurred between March and April. That is where we see the green bars change most drastically in height.
Subtract these monthly totals to calculate the decrease:
$44{,}482 − 34{,}727 = 9{,}755 \text{ units}$
We can visually deduce that the greatest decrease in Gizmos unit sales in consecutive months occurred between March and April. That is where we see the green bars change most drastically in height.
Subtract these monthly totals to calculate the decrease:
$44{,}482 − 34{,}727 = 9{,}755 \text{ units}$
Question 49 |
According to the frequency distribution chart shown below, how many students chose a favorite color other than Red, Green, or Blue?
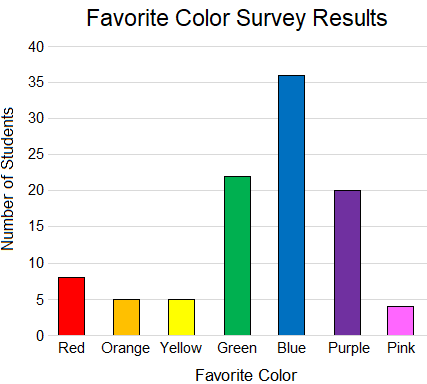
21 | |
57 | |
66 | |
17 | |
34 |
Question 49 Explanation:
The correct answer is (E). A favorite color “other than Red, Green, or Blue”, means that we are looking for the number of students who chose Orange, Yellow, Purple, or Pink.
Orange = 5 students
Yellow = 5 students
Purple = 20 students
Pink = 4 students
TOTAL of these 4 colors = 34 students
Orange = 5 students
Yellow = 5 students
Purple = 20 students
Pink = 4 students
TOTAL of these 4 colors = 34 students
Question 50 |
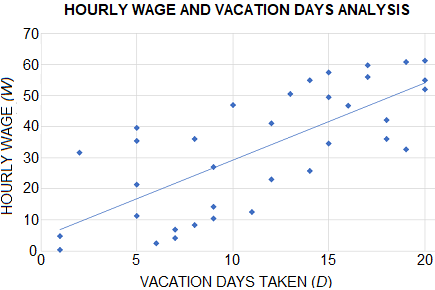
There are 35 data points shown in the scatter-plot below. What fraction of the data points represent an hourly wage (W) less than 50?
$\dfrac{33}{35}$ | |
$\dfrac{11}{35}$ | |
$\dfrac{32}{35}$ | |
$\dfrac{26}{35}$ | |
$\dfrac{14}{35}$ |
Question 50 Explanation:
The correct answer is (D). There are clearly more data points representing an hourly wage less than 50 than those representing a wage greater than or equal to 50.
Rather than count the number of data points with a wage less than 50, let’s save time and count the number of data points with a wage of 50 or greater and then deduct this from the 35 total points.
There are 9 such points (circled):
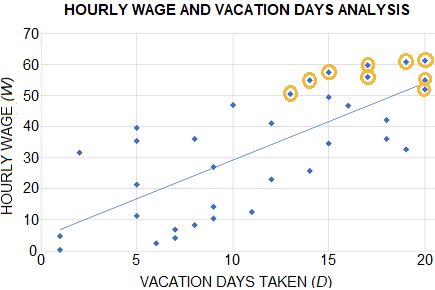
This means there are 26 (= 35 − 9) points representing a wage less than 50.
Since there are 35 total points, the fraction of data points representing an hourly wage less than 50 is $\frac{26}{35}$
Rather than count the number of data points with a wage less than 50, let’s save time and count the number of data points with a wage of 50 or greater and then deduct this from the 35 total points.
There are 9 such points (circled):
This means there are 26 (= 35 − 9) points representing a wage less than 50.
Since there are 35 total points, the fraction of data points representing an hourly wage less than 50 is $\frac{26}{35}$
Question 51 |
Two hundred attendees of a consumer electronics show were surveyed to find their preferred gaming system.
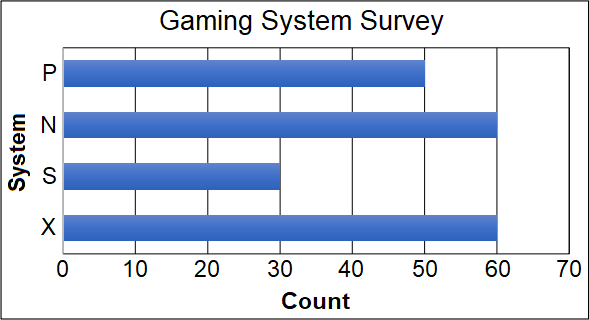
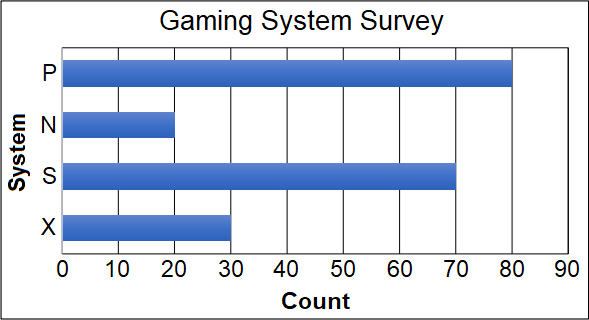
One-fifth of those who were surveyed preferred system “X.” Twice as many preferred system “N” as system “X.” Thirty fewer preferred system “S” compared to system “N.” The rest preferred system “P.”
Which bar graph correctly represents the results of the survey?
 | |
 | |
 | |
 | |
 |
Question 51 Explanation:
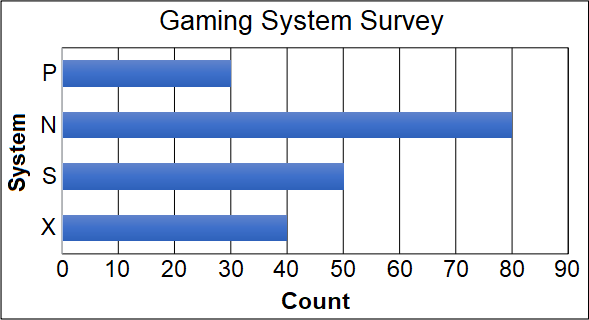
The correct answer is (A). There were 200 people surveyed. $\frac{1}{5}$ preferred system “X”. This means that $\frac{1}{5}*200 = 40$ people preferred system “X”.
Because only 1 of the 5 bar graphs has an “X” bar denoting 40, we actually have enough information to answer the question. However, for the sake of practice, we will look at calculating the remaining information:
Twice as many preferred “N” as “X”:
$N = 2 \ast X = 2 \ast 40 = 80$
30 fewer preferred “S” compared to“N”:
$S = X − 30 = 80 − 30 = 50$
The rest preferred “P” :
$P = 200 − X − N − S$
$P = 200 −40 − 80 − 50 = 30$
Because only 1 of the 5 bar graphs has an “X” bar denoting 40, we actually have enough information to answer the question. However, for the sake of practice, we will look at calculating the remaining information:
Twice as many preferred “N” as “X”:
$N = 2 \ast X = 2 \ast 40 = 80$
30 fewer preferred “S” compared to“N”:
$S = X − 30 = 80 − 30 = 50$
The rest preferred “P” :
$P = 200 − X − N − S$
$P = 200 −40 − 80 − 50 = 30$
Question 52 |
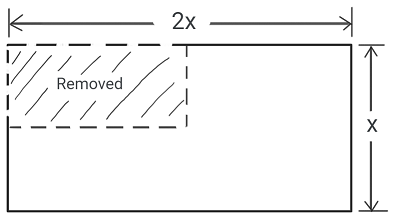
The figure below shows a rectangle with exactly one-quarter of it removed. After removing the upper-left quarter, the remaining shape has an area of 96 cm2. What is the value of $x$?
9 | |
4 | |
8 | |
10 | |
7 |
Question 52 Explanation:
The correct answer is (C). The area of the full rectangle, before the upper-left quarter is removed will be:
$A = 2x * x = 2x^2$
With one-quarter of the full rectangle removed, three-quarters of the full rectangle will remain. We are told that the area of the remaining three-quarters is 96 cm2.
$\dfrac{3}{4}A = 96$
$\dfrac{3}{4}(2x^2) = 96$
$2x^2 = \dfrac{4}{3}(96)$
$2x^2 = 128$
$x^2 = 64$
$x = 8$
(Must be positive since the lengths of the sides are positive.)
$A = 2x * x = 2x^2$
With one-quarter of the full rectangle removed, three-quarters of the full rectangle will remain. We are told that the area of the remaining three-quarters is 96 cm2.
$\dfrac{3}{4}A = 96$
$\dfrac{3}{4}(2x^2) = 96$
$2x^2 = \dfrac{4}{3}(96)$
$2x^2 = 128$
$x^2 = 64$
$x = 8$
(Must be positive since the lengths of the sides are positive.)
Question 53 |
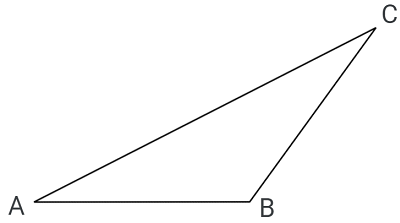
For the triangle shown below, $\overline{AB} \cong \overline{BC}$. If $∠B = 128^\circ$, what is the measure of $∠C\,?$
33° | |
26° | |
64° | |
52° | |
16° |
Question 53 Explanation:
The correct answer is (B). Since $\overline{AB} \cong \overline{BC}$, the triangle is isosceles and, therefore, the base angles are congruent: $∠A \cong ∠C$.
We also know that the angles of a triangle sum to 180°:
$m∠A+m∠B+m∠C =180^\circ$
$m∠A + 128^\circ + m∠C = 180^\circ$
Let $x$ be the measure of $∠A$. And, since $∠A \cong ∠C$, $x$ will also be the measure of $∠C$.
$m∠A + 128^\circ + m∠C = 180^\circ$
$x + 128 + x = 180$
$2x+128 = 180$
$2x = 52$
$x = 26$
$∠C = 26^\circ$
We also know that the angles of a triangle sum to 180°:
$m∠A+m∠B+m∠C =180^\circ$
$m∠A + 128^\circ + m∠C = 180^\circ$
Let $x$ be the measure of $∠A$. And, since $∠A \cong ∠C$, $x$ will also be the measure of $∠C$.
$m∠A + 128^\circ + m∠C = 180^\circ$
$x + 128 + x = 180$
$2x+128 = 180$
$2x = 52$
$x = 26$
$∠C = 26^\circ$
Question 54 |
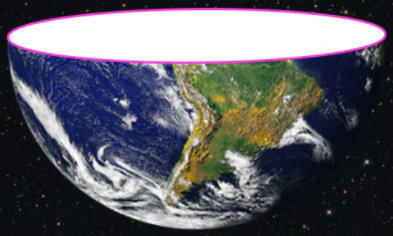
The length of the equator of the earth (shown in pink in the illustration below) is approximately 40,000 kilometers. Given that the equator represents the circumference of a circle with a diameter equal to the diameter of the earth, what is the approximate diameter of the earth?
15,000 km | |
13,000 km | |
19,000 km | |
17,000 km | |
11,000 km |
Question 54 Explanation:
The correct answer is (B). Recall that the circumference of a circle, $C$, can be expressed as: $C = π * D$
We are given that: $C = 40{,}000 \text{ km}$
$40{,}000 = π * D$
$D= \dfrac{40{,}000}{π}$
$D \approx 12{,}732$
$D \approx 13{,}000 \text{ km}$
We are given that: $C = 40{,}000 \text{ km}$
$40{,}000 = π * D$
$D= \dfrac{40{,}000}{π}$
$D \approx 12{,}732$
$D \approx 13{,}000 \text{ km}$
Question 55 |
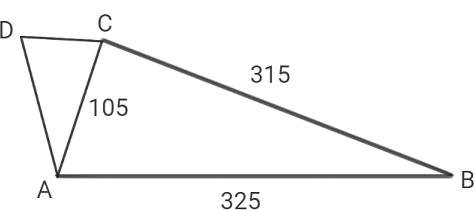
$∆ABC \sim ∆DAC$ (the triangles are similar).
What is the length of $\overline{DC}$?
35 | |
55 | |
45 | |
50 | |
40 |
Question 55 Explanation:
The correct answer is (A). When dealing with similar (or congruent) triangles, the order in which the triangles are labeled is very meaningful. For example, vertex $A$ of the first triangle corresponds to vertex $D$ of the second triangle; and side $\overline{BC}$ of the first triangle corresponds to side $\overline{AC}$ of the second triangle.
Also, for similar triangles the side lengths are proportional.
Based on these facts, we can set up an equivalent proportion:
$\dfrac{BC}{AC}=\dfrac{AC}{DC}$
$\dfrac{315}{105}=\dfrac{105}{DC}$
$(315)(DC) = (105)(105)$
$(315)(DC) = 11{,}025$
$DC = \dfrac{11{,}025}{315}$
$DC = 35$
Also, for similar triangles the side lengths are proportional.
Based on these facts, we can set up an equivalent proportion:
$\dfrac{BC}{AC}=\dfrac{AC}{DC}$
$\dfrac{315}{105}=\dfrac{105}{DC}$
$(315)(DC) = (105)(105)$
$(315)(DC) = 11{,}025$
$DC = \dfrac{11{,}025}{315}$
$DC = 35$
Question 56 |
In a survey of 100 people the following information was obtained: 40 like cats, 30 like both dogs and cats, and 20 do not like either dogs or cats. This information is shown in the diagram below.
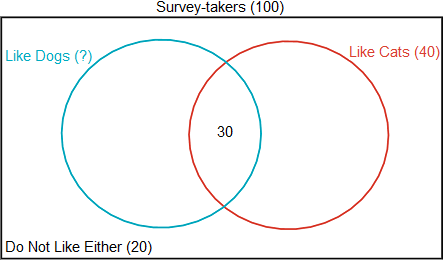
How many of those surveyed like dogs but not cats?
35 | |
25 | |
30 | |
40 | |
45 |
Question 56 Explanation:
The correct answer is (D).
Since 40 of those surveyed like cats, and of these 30 like both dogs and cats, then 40 − 30 = 10 must like cats but not like dogs, as shown (in green) below:
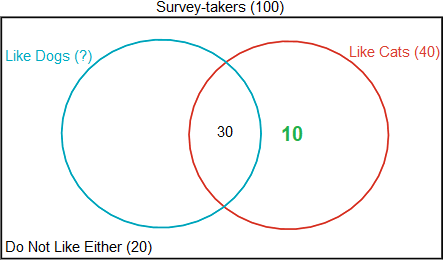
There were 100 surveyed in total and of these 20 did not like either dogs or cats, which means that 100 − 20 = 80 liked either dogs or cats or both.
“Liked Dogs (but not cats)” + “Liked Cats (but not dogs)” + “Liked Both” = 80
“Liked Dogs (but not cats)” + 10 + 30 = 80
“Liked Dogs (but not cats)” + 40 = 80
“Liked Dogs (but not cats)” = 40
The final Venn diagram is shown below:
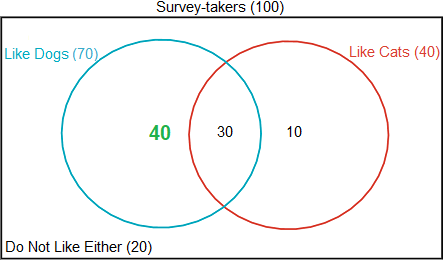
Since 40 of those surveyed like cats, and of these 30 like both dogs and cats, then 40 − 30 = 10 must like cats but not like dogs, as shown (in green) below:
There were 100 surveyed in total and of these 20 did not like either dogs or cats, which means that 100 − 20 = 80 liked either dogs or cats or both.
“Liked Dogs (but not cats)” + “Liked Cats (but not dogs)” + “Liked Both” = 80
“Liked Dogs (but not cats)” + 10 + 30 = 80
“Liked Dogs (but not cats)” + 40 = 80
“Liked Dogs (but not cats)” = 40
The final Venn diagram is shown below:
Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
There are 56 questions to complete.
|
List |